1012.至少有1位重复的数字

发表于 更新于 分类于 阅读次数：

前言

题目来自LeetCode：https://leetcode.cn/problems/numbers-with-repeated-digits/

题目（难度：困难）

给定正整数 n，返回在 [1, n] 范围内具有 至少 1 位 重复数字的正整数的个数。

示例1

输入：n = 20
输出：1
解释：具有至少 1 位重复数字的正数（<= 20）只有 11 。

示例 2：

输入：n = 100
输出：10
解释：具有至少 1 位重复数字的正数（<= 100）有 11，22，33，44，55，66，77，88，99 和 100 。

提示：

  • 1 <= n <= 10^9

题解

本题题目由于n过大，O(n)也会超出时间限制，即不能通过直接遍历得出答案，那么剩下的就是组合数学，一般组合数学的题目都可以用数位dp来解决。数位dp的介绍可以参考OI wiki。
本题要求至少有一位重复数字的数，分情况来说的话，有2个同、3个相同…k个相同(k小于等于n的位数)，正向思考的话情况过于复杂，不妨逆向思考，求出每个数位都不相同的数f，那么至少有一位重复数字的总数为n-f，因为这两种情况互补。

对位数进行dfs(深度搜索)，从高位一直到低位，当搜索到最后一位，返回1或0，表示找到了或没找到一个符合条件的数字。

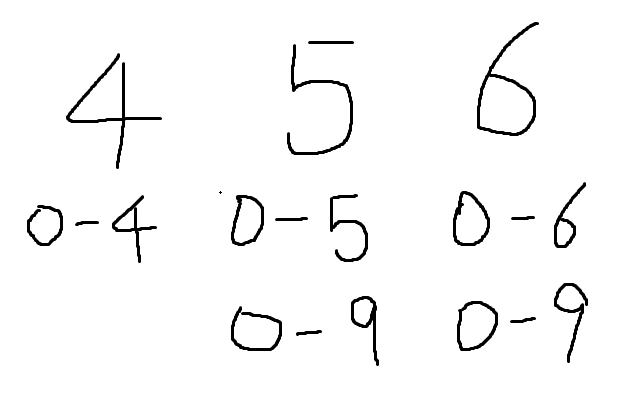
数位限制条件1

每位数字都有限制条件，如图，数字456，最高位可以填0-4(0可以代表没填或则前导0), 除去最高位后，都有两种情况(以次高位5做解释)：

  • 当前一位数取到n中对应位数的值(即最高位取到4)，那么当前位只能取到n中对应位数的值(5)，即上图中的第一个范围(0-5),因为这个数不能大于n。
  • 当前一位数没有取到n中对应位数的值(即最高位取到0-3)，那么当前位置没有限制(0-9)，即上图中第二个范围。

解决了第一个限制条件，则要考虑现在要求每个数位上的数都不相同的数，那么当搜索到第k个数位的时候必须知道前面的数位都取了什么，所以需要标记都取过哪些数，可以用一个set集合当标记，当然更好的方法是用一个数去标记(不用耗费额外的空间和时间去判断，加上后面需要记忆化的时候更简单)，这就涉及到二进制与集合的关系：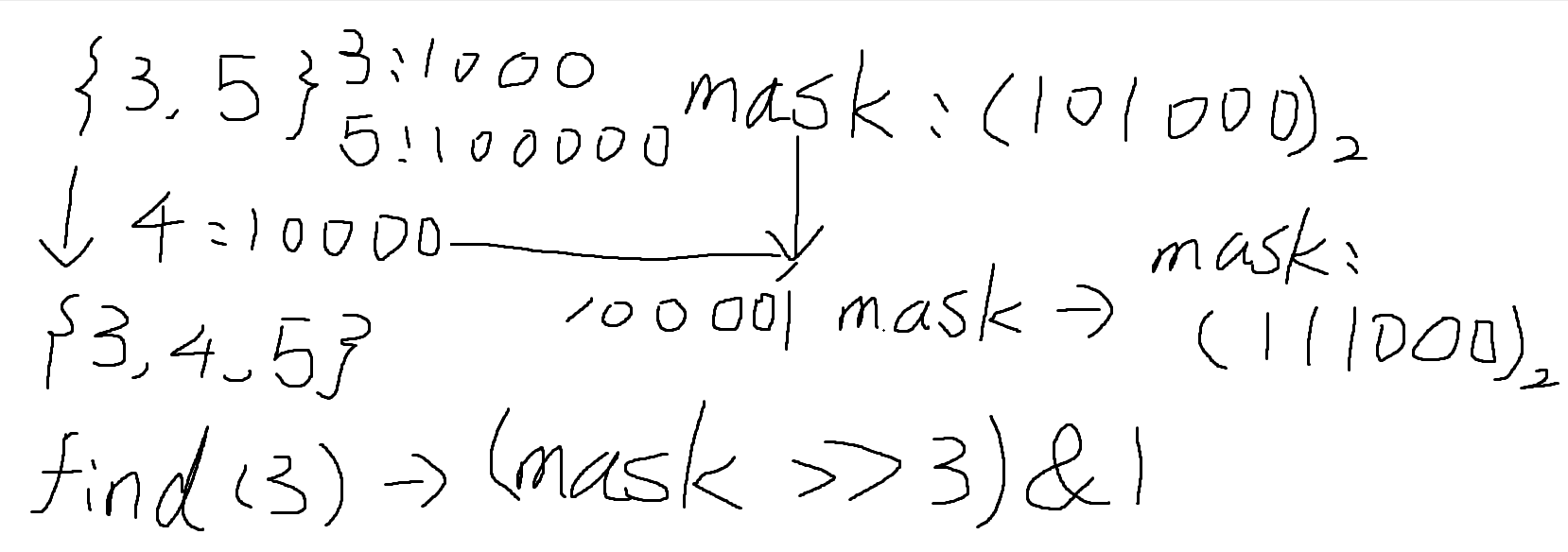
集合与位运算
因为这个集合只记录0-9十个数，所以可以用标记数mask的二进制数的位数代表0-9，从低位开始依次表示0-9，二进制数中1代表该位代表的数在集合里，否则不在集合里，例如(101000)2，从0开始从右往左数，第一个1在第四位，也就是代表3，第二个1在第六位，代表的是5，所以整个2进制数代表集合{3,5}，那么有如下操作：

  • 添加一个数k进集合：(1 << k) | mask，如上图，按添加4进集合{3,5}中为例子，1的二进制数为(0…01)2,左移4位后变成(0…010000)2,因为从低位从0开始，左移4位后，1的右面是有4个0，所以左移4位后就是在集合中代表4这个数，|(按位或操作)上mask后，mask为(111000)2，这时mask代表的集合为{3,4,5}。
  • 查询一个数k是否在集合中：(mask >> k) & 1,mask右移k位，相当让k+1位移动到最低位，&(按位与操作)上1后，相当于只保留最低位的值，如果是1，则代表k在集合中，否则代表k不在集合中。
  • 从集合中删除一个数k(本题没涉及删除操作)：((2^11-2) << k + 2^k - 1) & mask, 因为只有10个数，只需要10位表示，2^11-2的二进制是(1111111110)2,左移k位后再将左移产生的k个0填回1，即(1111011111)2，在&(按位与操作)mask，即可在集合中删除k。

当每一位取数的限制已经确定，那就可以递归遍历每一位数的情况，但是所有情况还是会超出时间的限制，仔细思考算12345和13345时，后面的345是重复计算的，可以用一个数组或则哈希表给他存起来，当再次需要用的时候再从里面取，而不是重新计算一次，这样就可以大大降低所需要的时间，这称为记忆化搜索。对于本题，需要记录的是当递归到第i位时，集合mask所得的结果。

构造递归函数f：f(int i, int mask, boolean isLimit, boolean isNum)

  • i：当前搜索的位数
  • mask：所取过的数的集合
  • isLimit：是否受限制，也就是取0-9还是0-n中第i位的数。当为false时，代表不受限制，可以取0-9，否则就是另外一种情况
  • isNum：前面是否有填过数，当前面全0时，代表没填过数，如果前面全为0时(也就是为false)，有两种情况，当前位填0代表跳过当前位，如果是0以外则是该位不跳过。

递归结束标志：当i等与n的总位数时
初始状态：f(0,0,true,false)，从第1位开始，由于方便记忆数组，所以下标从0开始，mask一开始空集，自然为0，第一位数是一定受限制的，一开始没填数，所以isNum也是false；

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
class Solution {
    char[] s;
    //保存计算过的结果
    int[][] dp;

    public int numDupDigitsAtMostN(int n) {
        //将数字转化成字符串，便于操作
        s = String.valueOf(n).toCharArray();
        //dp[i][mask] 代表第i位选了mask集合的结果
        dp = new int[s.length][1 << 10];
        for (int i = 0; i < s.length; i++) {
            Arrays.fill(dp[i], -1);
        }
        return n - f(0, 0, true, false);
    }

    //递归函数
    public int f(int i, int mask, boolean isLimit, boolean isNum) {
        //递归结束条件
        if(i == s.length){
            //如果是一个合法的数则返回1
            return isNum ? 1 : 0;
        }
        //当要计算的结果在dp中，直接用
        if(!isLimit && isNum && dp[i][mask] != -1){
            return dp[i][mask];
        }
        int res = 0;
        //如果前面没有填过数，这是第一种情况填0，跳过当前位
        if(!isNum){
            res = f(i + 1, mask, false, false);
        }
        //确定上限
        int up = isLimit ? (s[i] - '0') : 9;
        //遍历可能能取的数，当isNum为false时，进入第二种情况，不跳过，也就是从1开始，
        //当isNum为true时，代表前面填过数，不必区分下限
        for(int k = isNum ? 0 : 1; k <= up; k++){
            //判断当前要取的数是否在集合里，也就是判断之前取过没有
            if((mask >> k & 1) == 0){
                //mask|(1<<k)是将k加到集合中去，下一位受到限制的条件是当前位受限制并且当前位取得是上限
                res += f(i + 1, mask | (1 << k), isLimit && k == up, true);
            }
        }
        //如果该值没有被记录过，则记录
        if(dp[i][mask] == -1){
            dp[i][mask] = res;
        }
        return res;
    }
}