2488.统计中位数为K的子数组

发表于 分类于 阅读次数：

前言

题目来自LeetCode：https://leetcode.cn/problems/count-subarrays-with-median-k/

题目（难度：困难）

给你一个长度为 n 的数组 nums ，该数组由从 1 到 n 的 不同 整数组成。另给你一个正整数 k 。
统计并返回 nums 中的 中位数 等于 k 的非空子数组的数目。
注意：

  • 数组的中位数是按 递增 顺序排列后位于 中间 的那个元素，如果数组长度为偶数，则中位数是位于中间靠 左 的那个元素。
    • 例如，[2,3,1,4] 的中位数是 2 ，[8,4,3,5,1] 的中位数是 4 。
  • 子数组是数组中的一个连续部分。
    示例1：
    1
    2
    3
    输入：nums = [3,2,1,4,5], k = 4
    输出：3
    解释：中位数等于 4 的子数组有：[4]、[4,5] 和 [1,4,5] 。
    提示：
  • n == nums.length
  • 1 <= n <= 10^5
  • 1 <= nums[i], k <= n
  • nums 中的整数互不相同

题解

本题要求中位数为k的子数组，那么子数组一定包含k，所有可以k为分割点将数组nums分成左右两部分，假设k所在的下标为index，那么子数组的数目为(index + 1) * (nums.length - index + 1)。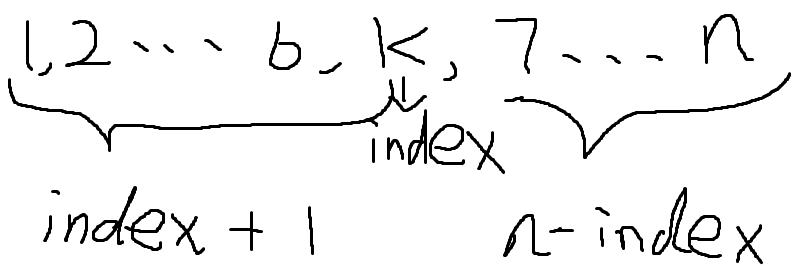
子数组图解
当只考虑左边，子数组有{k},{6,k}…{2,…6,k},{1,2,…6,k}共index + 1个，右边也一样，{7}…{7,…n}共(nums.length - index)个，不用右边的或则在右边挑一个与左边配合则是一个子数组，那么子数组的个数就是(index + 1) * (nums.length - index + 1)。
我们只需要将所有子数组都判定一次，是否以k为中位数即可，若k为中位数，那么大于k的数目等于小于k的数目，所以我们只需要判断子数组中有多少个数大于k，有多少个小于k。（题目说明当为偶数的时候中间靠左的为中位数，也就是说大于k的数目可以比小于k的数目多1）
最简单的是，两层循环，外层循环遍历k的右边，内层循环遍历k的左边，只要当大于k的数目减去小于k的数目等于0或者1时，则为符合题意的子数组。很遗憾的是，最坏的情况下，即k的左右两边数目相等的时候，时间复杂度来到了O(n^2),在n=10^5时会超出时间限制。
那么，常用的处理方法是将任意一边的情况存进哈希表，遍历另外一边，每次判断哈希表中是否存在满足题意的情况，这样时间复杂度无论k在哪里都是O(n)。

代码 O(n)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class Solution {
    public int countSubarrays(int[] nums, int k) {
        //储存大于k（小于k）的个数
        HashMap<Integer, Integer> map = new HashMap<>();
        
        int index = -1;
        //找到k的位置
        for(int i = 0; i < nums.length; i++){
            if(nums[i] == k){
                index = i;
                break;
            }
        }

        int i = index - 1;
        //当d>0 d则为大于k的个数，d=0, 大于k的个数与小于k的个数相等，d<0 |d|则为小于k的个数
        int d = 0;
        //{k} 自然是符合题目的子数组
        map.put(0, 1);
        //遍历左边
        while(i >= 0){
            //大于k d加1， 小于k d-1
            if(nums[i] > nums[index]){
                d++;
            }else{
                d--;
            }
            //并且把每个情况存进哈希表
            map.put(d, map.getOrDefault(d, 0) + 1);
            i--;
        }

        d = 0;
        //不取右边任何数，符合的个数
        int res = map.getOrDefault(0, 0) + map.getOrDefault(1, 0);
        for(i = index + 1; i < nums.length; i++){
            if(nums[i] > nums[index]){
                d++;
            }else{
                d--;
            }
            //当左右两边大于k个数减去小于k的个数的差为0或则1的时候符合题意
            res += map.getOrDefault(0 - d, 0) + map.getOrDefault(1 - d, 0);
        }

        return res;
    }
}