前言
题目来自LeetCode:https://leetcode.cn/problems/maximal-network-rank/
题目(难度:中等)
n 座城市和一些连接这些城市的道路 roads 共同组成一个基础设施网络。每个 roads[i] = [ai, bi] 都表示在城市 ai 和 bi 之间有一条双向道路。
两座不同城市构成的 城市对 的 网络秩 定义为:与这两座城市 直接 相连的道路总数。如果存在一条道路直接连接这两座城市,则这条道路只计算 一次 。
整个基础设施网络的 最大网络秩 是所有不同城市对中的 最大网络秩 。
给你整数 n 和数组 roads,返回整个基础设施网络的 最大网络秩 。
示例1
![示例1]()
1
2
3
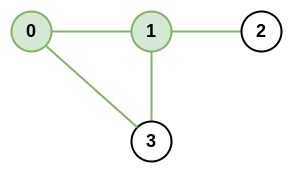
| 输入:n = 4, roads = [[0,1],[0,3],[1,2],[1,3]]
输出:4
解释:城市 0 和 1 的网络秩是 4,因为共有 4 条道路与城市 0 或 1 相连。位于 0 和 1 之间的道路只计算一次。
|
提示:
- 2 <= n <= 100
- 0 <= roads.length <= n * (n - 1) / 2
- roads[i].length == 2
- 0 <= ai, bi <= n-1
- ai != bi
- 每对城市之间 最多只有一条 道路相连
题解
本题考的是图的度(degree),只要找到度最大和次大的结点,即为答案。因为同一条边只算一次,如果两结点之间有边,则需要减去1。由于本题2 <= n <= 100, 直接遍历节点对即可。若n的值大于达到10^5时,即O(n^2)超出时间限制时,那就需要用贪心方法在O(n)的时间复杂度内找出度最大和次大的两个结点。
代码
遍历结点对O(n^2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| class Solution {
public int maximalNetworkRank(int n, int[][] roads) {
HashMap<Integer, HashSet<Integer>> map = new HashMap<>();
for(int i = 0; i < n; i++){
HashSet<Integer> t = new HashSet<>();
map.put(i, t);
}
for(int i = 0; i < roads.length; i++){
int u = roads[i][0];
int v = roads[i][1];
map.get(u).add(v);
map.get(v).add(u);
}
int max = -1;
for(int i = 0; i < n; i++){
for(int j = i + 1; j < n; j++){
int cul = map.get(i).size() + map.get(j).size();
if(map.get(i).contains(j)){
cul--;
}
max = max > cul ? max : cul;
}
}
return max;
}
}
|
贪心O(n)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
| class Solution {
public int maximalNetworkRank(int n, int[][] roads) {
HashMap<Integer, HashSet<Integer>> map = new HashMap<>();
for(int i = 0; i < n; i++){
HashSet<Integer> t = new HashSet<>();
map.put(i, t);
}
for(int i = 0; i < roads.length; i++){
int u = roads[i][0];
int v = roads[i][1];
map.get(u).add(v);
map.get(v).add(u);
}
int max = -1;
int smax = -1;
List<Integer> maxArr = new ArrayList<>();
List<Integer> smaxArr = new ArrayList<>();
for(int i = 0; i < n; i++){
int cur = map.get(i).size();
if(cur > max){
smax = max;
smaxArr = new ArrayList<>(maxArr);
max = cur;
maxArr.clear();
maxArr.add(i);
}else if(cur == max){
maxArr.add(i);
}else if(cur > smax){
smaxArr.clear();
smaxArr.add(i);
smax = cur;
}else if(cur == smax){
smaxArr.add(i);
}
}
if(maxArr.size() == 1){
int first = maxArr.get(0);
for(int i : smaxArr){
if(!map.get(first).contains(i)){
return max + smax;
}
}
return max + smax - 1;
}else{
int size = maxArr.size();
if(size * (size - 1) / 2 > roads.length){
return max * 2;
}
for(int u : maxArr){
for(int v : maxArr){
if(u != v && !map.get(u).contains(v)){
return max * 2;
}
}
}
return max * 2 - 1;
}
}
}
|